6.2 Solution

To me the shape that resembles the droplet the most is sphere. Luckily, it also got well defined formulas for surface area and volume (see the link above), so this is what we will use in our solution.

struct Sphere
    radius::Flt
    Sphere(r::Flt) = r <= 0 ? error("radius must be > 0") : new(r)
end

# formula from Wikipedia
function getVolume(s::Sphere)::Flt
    return (4/3) * pi * s.radius^3
end

# formula from Wikipedia
function getSurfaceArea(s::Sphere)::Flt
    return 4 * pi * s.radius^2
end

Now, let’s define a big lipid droplet with a radius of, let’s say, 10 [μm].

bigS = Sphere(10.0) # 10 um
bigV = getVolume(bigS)
bigA = getSurfaceArea(bigS)

bigV

4188.790204786391

In the next step we will split this big droplet into a few smaller ones of equal sizes. Splitting the volume is easy, we just divide bigV by n droplets. However, we need a way to determine the size (radius) of each small droplet. Let’s try to transform the formula for a sphere’s volume and see if we can get radius from that.

\[ v = \frac{4}{3} * \pi * r^3 \qquad{(4)}\]

If a = b, then b = a, so we may swap sides.

\[ \frac{4}{3} * \pi * r^3 = v \qquad{(5)}\]

The multiplication is commutative (the order does not matter), i.e. 2 * 3 * 4 is the same as 4 * 3 * 2 or 2 * 4 * 3, therefore we can rearrange elements on the left side of Equation 5 to:

\[ r^3 * \frac{4}{3} * \pi = v \qquad{(6)}\]

Now, one by one we can move *\(\frac{4}{3}\) and *\(\pi\) to the right side of Equation 6. Of course, we change the mathematical operation to the opposite (division instead of multiplication) and get:

\[ r^3 = v / \frac{4}{3} / \pi \qquad{(7)}\]

All that’s left to do is to move exponentiation (\(x^3\)) to the right side of Equation 7 while changing it to the opposite mathematical operation (cube root, i.e. \(\sqrt[3]{x}\)).

\[ r = \sqrt[3]{v / \frac{4}{3} / \pi} \qquad{(8)}\]

Now, you might wanted to quickly verify the solution using Symbolic.symbolic_linear_solve we met in Section 3.2. Unfortunately, we cannot use r^3 (r to the 3rd power) as an argument (and solve for r), since then it wouldn’t be a linear equation (to be linear the maximum power must be equal to 1) required by _linear_solve. We could have used other, more complicated solver, but instead we will keep things simple and apply a little trick:

import Symbolics as Sym

# fraction - 4/3, p - π, r3 - r^3, v - volume
Sym.@variables fraction p r3 v
Sym.symbolic_linear_solve(fraction * p * r3 ~ v, r3)

v / (fraction*p)

So, instead of writing the formula as it is, we just named our variables fraction, p, r3 and v. Anyway, according to Sym.symbolic_linear_solve \(r^3 = v / (\frac{4}{3} * \pi)\), which is actually the same as Equation 7 above [since e.g. 18 / 2 / 3 == 18 / (2 * 3)]. Ergo, we may be fairly certain we correctly solved Equation 7 and therefore Equation 8.

Once, we confimed the validity of the formula in Equation 8, all that’s left to do is to translate it into Julia code.

function getSphere(volume::Flt)::Sphere
    # cbrt - fn that calculates cube root of a number
    radius::Flt = cbrt(volume / (4/3) / pi)
    return Sphere(radius)
end

Note: If there were no function for \(\sqrt[3]{x}\) you could easily define it yourself with: getCbrt(x) = x^(1/3) (here I used a single expression function for brevity) since \(\sqrt[n]{x} = x^{1/n}\).

Time to test how it works. Let’s see if we can divide bigS (actually its volume: bigV) into 4 smaller drops of total volume equal to bigV.

# isapprox compares variables for equality
# accounts for possible rounding error
isapprox(
    getSphere(bigV / 4) |> getVolume,
    bigV / 4
)

true

Once we got that working, we evaluate the total area of the droplets of different size.

sumsOfAreas = [bigA]
sumsOfVolumes = [bigV]
radii = [bigS.radius]

numsOfDroplets = collect(4:4:12)
for nDrops in numsOfDroplets
    # local variables smallS, smallV, smallA, sumSmallAs, sumSmallVs
    # visible only in for loop
    smallS = getSphere(bigV / nDrops)
    smallV = getVolume(smallS)
    smallA = getSurfaceArea(smallS)
    sumSmallAs = smallA * nDrops
    sumSmallVs = smallV * nDrops
    push!(sumsOfAreas, sumSmallAs)
    push!(sumsOfVolumes, sumSmallVs)
    push!(radii, smallS.radius)
end

prepend!(numsOfDroplets, 1)

We begin by initializing vectors that will hold the sumsOfAreas, sumsOfvolumes, and radii of our lipid droplets. Then we define the number of droplets that we want to split our big droplet into (numsOfDroplets). For each of those (for nDrops in numsOfDroplets) we determine the radius (smallS = getSphere), volume (smallV) and surface area (smallA) of a single small droplet as well as total area (sumSmallAs) and total volume (sumSmallVs) of nDrops. We add the total area, total volume and radius of a single droplet to the sumsOfAreas, sumsOfVolumes, and radii vectors, respectively. In the end we prepend 1 to the numOfDroplets, since we started with one big droplet (bigS).

BTW. Notice that smallS, smallV, smallA, sumSmallAs, sumSmallVs are all local variables defined for the first time in the for loop and visible only inside of it. If you try to print out their values outside of the loop you will get an error like ERROR: UndefVarError: 'smallS' not defined.

Anyway, now, we can either examine the vectors (sumsOfAreas, sumsOfVolumes, radii, numOfDroplets) one by one, or do one better and present them on a graph with e.g. CairoMakie (I’m not going to explain the code below, for reference see my previous book or CairoMakie tutorial).

import CairoMakie as Cmk

fig = Cmk.Figure();
ax = Cmk.Axis(fig[1, 1],
              title="Lipid droplet size vs. summaric surface area",
              xlabel="number of lipid droplets",
              ylabel="total surface area [μm²]", xticks=0:13);
Cmk.scatter!(ax, numsOfDroplets, sumsOfAreas, markersize=radii .* 5,
             color="gold1", strokecolor="black");
Cmk.xlims!(ax, -3, 16);
Cmk.ylims!(ax, 800, 3000);
Cmk.text!(ax, numsOfDroplets, sumsOfAreas .- 150,
    text=map(r -> "single droplet radius = $(round(r, digits=2)) [μm]",
             radii),
    fontsize=12, align=(:center, :center)
);
Cmk.text!(ax, numsOfDroplets, sumsOfAreas .- 250,
    text=map((v, n) ->
    "volume ($n droplet/s) = $(round(v, digits=2)) [μm³]",
    sumsOfVolumes, numsOfDroplets),
    fontsize=12, align=(:center, :center)
);
fig

Behold.

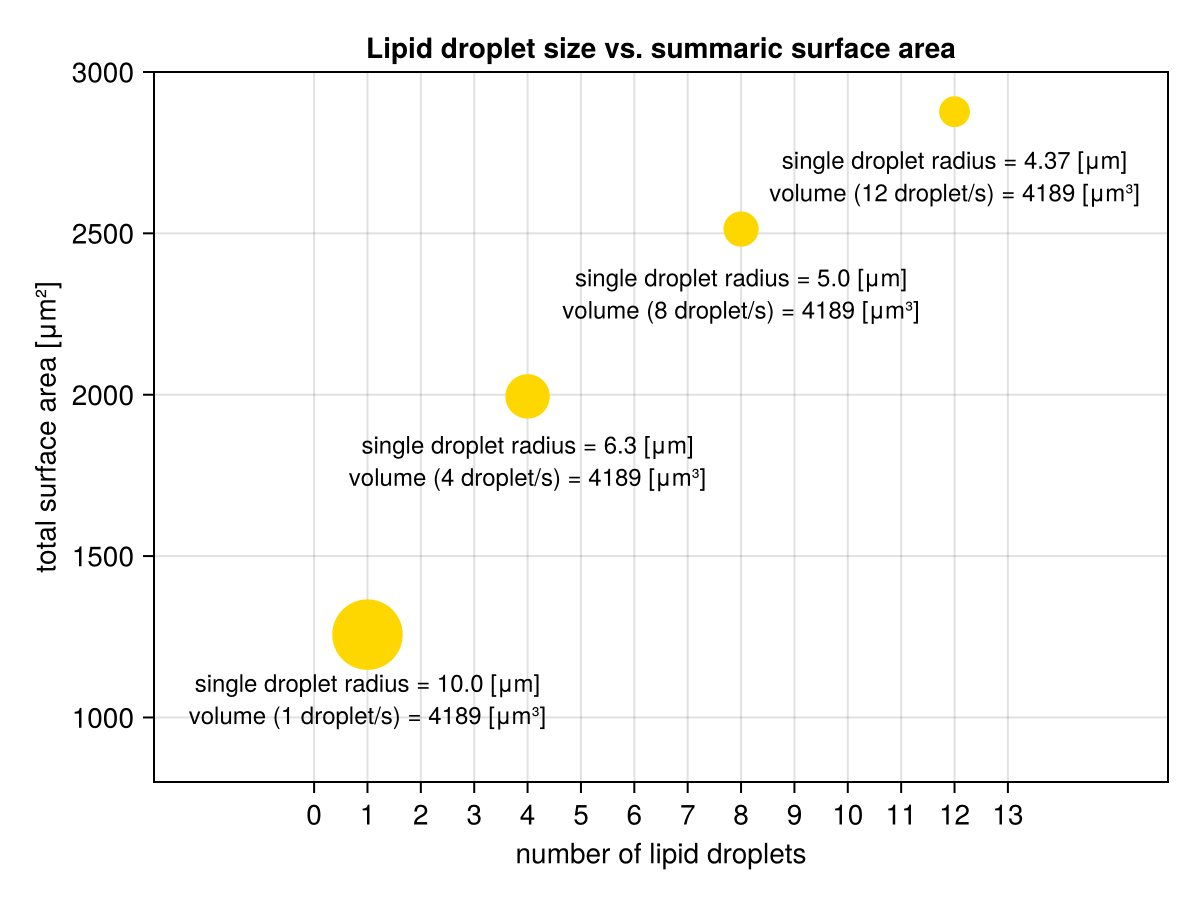
So it turns out that what they taught me in the school all those years ago is actually true. But only now I can finally see it. Nice.