9.2 Solution

If you read the Wikipedia’s description of the Pascal’s triangle then you may have noticed this cool animation (see below).

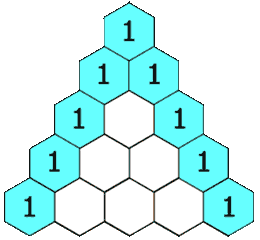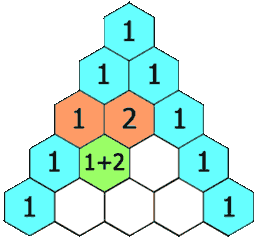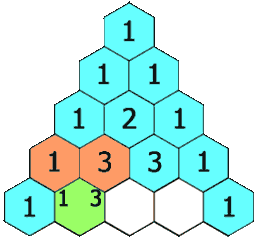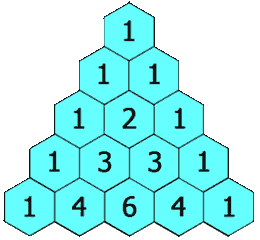
It indicates that in order to create a new row of the triangle you just take the previous row and add pair of its elements together to create the next row. Finally, at the edges of the new row you place 1s. So let’s start by doing just that.

function getSumOfPairs(prevRow::Vec{Int})::Vec{Int}
    @assert all(prevRow .> 0) "every element of prevRow must be > 0"
    return [a + b for (a, b) in zip(prevRow, prevRow[2:end])]
end

function getRow(prevRow::Vec{Int})::Vec{Int}
    @assert length(prevRow) > 1 "length(prevRow) must be > 1"
    sumsOfPairs::Vec{Int} = getSumOfPairs(prevRow)
    return [1, sumsOfPairs..., 1]
end

The first function (getSumOfPairs) creates pairs of values based on the previous row (prevRow). It returns a vector of tuples of (a, b) that are the elements from the zipped vectors, e.g.

zip([1, 2, 3, 4], [2, 3, 4]) |> collect

(1, 2)

(2, 3)

(3, 4)

Notice, that the second argument to zip is its first element ([1, 2, 3, 4]) with shift 1 (just like prevRow[2:end] in the body of getSumOfPairs) and the parallel elements from both the vectors are zipped together as long as there are pairs. Next, the numbers in a pair are added (a + b in the body of getSumOfPairs). Finally, getRow uses the sumsOfPairs and adds 1s on the edges. The ... in getRow unpacks elements from a vector, i.e. [1, [3, 2]..., 1] becomes [1, 3, 2, 1]. All in all, we got a pretty faithful translation of the algorithm (from Figure 3) to Julia.

Now we are ready to build the triangle row by row.

function getPascalTriangle(n::Int)::Vec{Vec{Int}}
    @assert 0 <= n <= 10 "n must be in range [0-10]"
    triangle::Dict{Int, Vec{Int}} = Dict(0 => [1], 1 => [1, 1])
    if !haskey(triangle, n)
        for row in 2:n
            triangle[row] = getRow(triangle[row-1])
        end
    end
    return [triangle[k] for k in 0:n]
end

We define our triangle with initial two rows. Next, we move downwards through the possible triangle rows (for row in 2:n) and build the next row based on the previous one getRow(triangle[row-1]). All that’s left to do is to return the triangle as a vector of vectors (Vec{Vec{Int}})) which will give us a right triangle printed in the output by default. For instance, let’s get the Pascal’s triangle from Figure 3.

getPascalTriangle(4)

[1]

[1, 1]

[1, 2, 1]

[1, 3, 3, 1]

[1, 4, 6, 4, 1]

Pretty neat, we could stop here or try to add some text formatting. In order to do that we will need some way to determine the length of an integer when printed (getNumLen below) as well as the maximum number length in a Pascal’s triangle. The latter can be done by examining its last (longest) row, hence getMaxNumLen below accepts a vector.

function getNumLen(n::Int)::Int
    return n |> string |> length
end

function getMaxNumLen(v::Vec{Int})::Int
    return map(getNumLen, v) |> maximum
end

Once we got it, we need a way to center a number or a row (represented as a string).

function center(sth::A, totLen::Int)::Str where A<:Union{Int, Str}
    s::Str = string(sth)
    len::Int = length(s)
    @assert totLen > 0 && len > 0 "both totLen and len must be > 0"
    @assert totLen >= len "totLen must be >= len"
    diff::Int = totLen - len
    leftSpaceLen::Int = round(Int, diff / 2)
    rightSpaceLen::Int = diff - leftSpaceLen
    return " " ^ leftSpaceLen * s * " " ^ rightSpaceLen
end

In order to center its input (sth - an integer or a string) the function determines the difference (diff) between the length (totLen) of the desired result and the actual length of s. The difference is split roughly in half (leftSpaceLen and rightSpaceLen) and glued together with s using string concatenation (*) and exponentiation (^) that we met in Section 8.2. Due to the limited resolution offered by the text display of a terminal the result is expected to be slightly off on printout, but I think we can live with that.

Time to format a row.

function getFmtRow(
    row::Vec{A}, numLen::Int, rowLen::Int)::Str where A<:Union{Int, Str}
    fmt(num) = center(num, numLen)
    formattedRow::Str = join(map(fmt, row), " ")
    return center(formattedRow, rowLen)
end

For that we just map a formatter (fmt) over every element of the row and join the resultant vector of strings intercalating its elements with space (" "). Finally, we center the formattedRow to the desired length (rowLen).

All that’s left to do is to get a formatted triangle.

function getFmtPascTriangle(n::Int, k::Int)::Str
    @assert n >= 0 && k >= 0 "n and k must be >= 0"
    @assert n <= 10 && k <= 10 "n and k must be <= 10"
    @assert n >= k "n must be >= k"
    triangle::Vec{Vec{Int}} = getPascalTriangle(n)
    lastRow::Vec{Int} = triangle[end]
    maxNumWidth::Int = getMaxNumLen(lastRow) + 1
    lastRowWidth::Int = (n+1) * maxNumWidth + n
    fmtRow(row) = getFmtRow(row, maxNumWidth, lastRowWidth)
    formattedTriangle::Str = join(map(fmtRow, triangle), "\n")
    indicators::Vec{Str} = fill(" ", n+1)
    indicators[k+1] = "∆"
    return formattedTriangle * "\n" * fmtRow(indicators)
end

Since getFmtPascTriangle is a graphical equivalent of binomial(n, k) then it’s only fitting to accept the two letters as its input. We begin by obtaining the triangle, its lastRow and based on it the maximum width of a number in the triangle (maxNumWidth, +1 produces more pleasing output). Next, we determine the width of the last row. Notice the n+1 part (here and below in the function) as well as k+1 part later on. In, general Julia and humans count elements starting from 1, whereas a Pascal’s triangle is 0 indexed, hence we added +1 to help us translate one system into the other. Anyway, the length of lastRow (the longest row in triangle) is the number of digits in the row ((n+1)) times the width of a formatted digit (maxNumWidth) plus the number of spaces between the formatted digits. The number of spaces is 1 less than the number of slots, e.g., humans got 5 fingers, and 4 spaces between them, hence here we used +n since the number of digits was (n+1). Next, we obtain the formattedTriangle by maping fmtRow on its each row and separating the rows with newlines (\n). We finish, by adding the indicator ("∆") under our k and voila, we are finally ready to answer our question.

# how many different teams of 5 players
# can we compose out of 9 candidates?
getFmtPascTriangle(9, 5)

                        1
                      1    1
                    1    2    1
                 1    3    3    1
              1    4    6    4    1
            1    5   10   10    5    1
          1    6   15   20   15    6    1
       1    7   21   35   35   21    7    1
    1    8   28   56   70   56   28    8    1
  1    9   36   84  126  126   84   36    9    1
                           ∆

Wow, 126. Who would have thought. Just in case let’s compare the output with the built in binomial (compare with the last row of the triangle).

binomial.(9, 0:9)

[1, 9, 36, 84, 126, 126, 84, 36, 9, 1]

So, I guess our triangle works right. Actually the two edge cases are easy enough for us to check them in our heads. For instance, how many different teams of 0 players can we compose out of 9 candidates? Well, there is only one way to do that (1 in the bottom row, first from the left), by not choosing any player at all. And how many different teams of 1 player can we compose of 9 candidates? Well, nine teams (9 in the bottom row, second from the left) because each player would compose one separate team.