22.2 Solution

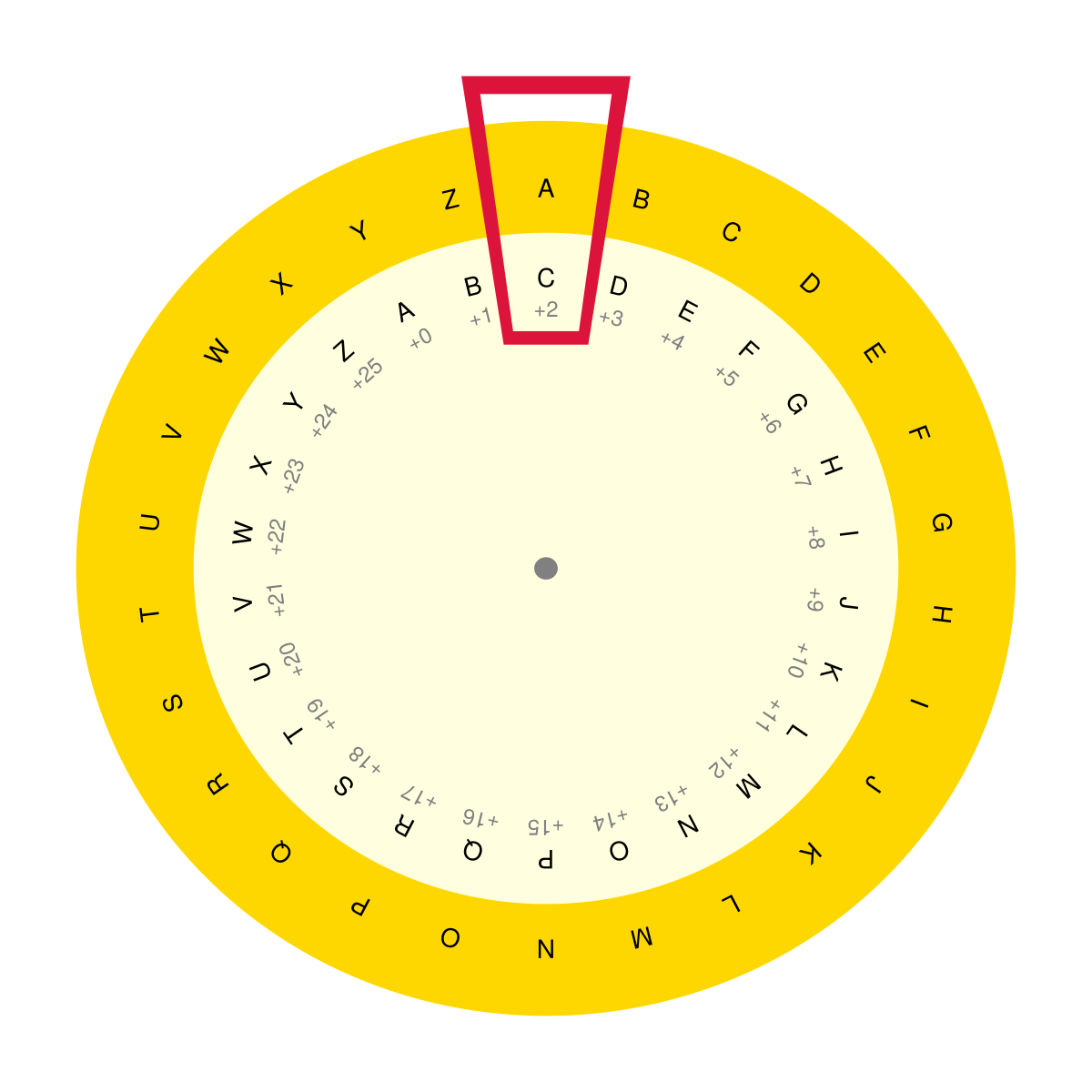
Let’s start by writing a function that will create alphabets for the outer and inner rings of the discs from Figure 13.

function getAlphabets(rotBy::Int, upper::Bool)::Tuple{Str, Str}
    alphabet::Str = upper ? join('A':'Z') : join('a':'z')
    rot::Int = abs(rotBy) % length(alphabet)
    rotAlphabet::Str = alphabet[(rot+1):end] * alphabet[1:rot]
    return rotBy < 0 ? (rotAlphabet, alphabet) : (alphabet, rotAlphabet)
end

First we create an alphabet made of 'a' to 'z' letters with the desired casing (upper) using a StepRange ('a':'z' or 'A':'Z') that we join into a string. Next, we use modulo operator (% - returns reminder of a division) to get the desired rotation (rot). This allows us to gracefully handle the overflow of rotBy [e.g. when rotBy is 28 and length(alphabet) is 26 we get 28 % 26i.e. 2 (full circle turn + shift by 2 fields)]. Then we create the rotated alphabet (rotAlphabet) starting at (rot+1) and appending (*) the beginning of the normal alphabet. Finally, if rotBy is negative (rotBy < 0, decrypting the message) we return rotAlphabet and alphabet to be used as outer and inner disc in Figure 13, respectively. Otherwise alphabet lands in the outer ring and ‘rotAlphabet’ in the inner one.

Time for a simple test.

Dict(i => getAlphabets(i, true) for i in -1:1:1)

Dict{Int64, Tuple{String, String}} with 3 entries:
  0 => ("ABCDEFGHIJKLMNOPQRSTUVWXYZ", "ABCDEFGHIJKLMNOPQRSTUVWXYZ")
  -1 => ("BCDEFGHIJKLMNOPQRSTUVWXYZA", "ABCDEFGHIJKLMNOPQRSTUVWXYZ")
  1 => ("ABCDEFGHIJKLMNOPQRSTUVWXYZ", "BCDEFGHIJKLMNOPQRSTUVWXYZA")

Appears to be working as intended. Now, even a greatest journey begins with a first step. Therefore, in order to encode any text we need to be able to encode a single character.

function codeChar(c::Char, rotBy::Int)::Char
    outerDisc::Str, innerDisc::Str = getAlphabets(rotBy, isuppercase(c))
    ind::Union{Int, Nothing} = findfirst(c, outerDisc)
    return isnothing(ind) ? c : innerDisc[ind]
end

codeChar (generic function with 1 method)

We begin by obtaining outerDisc and innerDisc with getAlphabets that we just created. Next, we search for the index (ind) of the character to encode (c) in the outerDisc. The search may fail (e.g. no , in an alphabet) so ind can be either nothing (value nothing of type Nothing indicates a failure) or an integer hence the type of ind is Union{Int, Nothing} to depict just that. Finally, if the search failed (isnothing(ind)) we just return c as it was, otherwise we return the encoded letter read from the inner ring (innerDisc[ind]). Observe.

(
    codeChar('a', 1),
    codeChar('A', 2),
    codeChar(',', 2)
)

('b', 'C', ',')

Once we know how to code a character, time to code a string.

# rotBy > 0 - encrypting, rotBy < 0 - decrypting, rotBy = 0 - same msg
function codeMsg(msg::Str, rotBy::Int)::Str
    coderFn(c::Char)::Char = codeChar(c, rotBy)
    return map(coderFn, msg)
end

And voila. Notice, that first we created coderFn, which is a function (single expression function) inside of a function (codeMsg). Now we can neatly use it with map.

OK, time to decipher our enigmatic message (remember that in Section 21.2 we figured out that the shift is equal 13).

# be sure to adjust the path
# the file's size is roughly 31 KiB
codedTxt = open("./code_snippets/shift/trarfvf.txt") do file
    read(file, Str)
end

decodedTxt = codeMsg(codedTxt, -13)
"<<" * first(decodedTxt, 54) * ">>"

<<In the beginning God created the heaven and the earth.>>

Hmm, it looks suspiciously like the first phrase from the Bible.

codeMsg("trarfvf", -13)

genesis

And indeed, even the file name indicates that it is (a part of) the Book of Genesis.

We could stop here or try to improve our solution a bit.

Let’s try to define getEncryptionMap that will be an equivalent of our getAlphabets.

function getEncryptionMap(rotBy::Int)::Dict{Char, Char}
    encryptionMap::Dict{Char, Char} = Dict()
    alphabet::Str = join('a':'z')
    rot::Int = abs(rotBy) % length(alphabet)
    rotAlphabet::Str = alphabet[(rot+1):end] * alphabet[1:rot]
    if rotBy < 0
        alphabet, rotAlphabet = rotAlphabet, alphabet
    end
    for i in eachindex(alphabet)
        encryptionMap[alphabet[i]] = rotAlphabet[i]
        encryptionMap[uppercase(alphabet[i])] = uppercase(rotAlphabet[i])
    end
    return encryptionMap
end

The function is pretty similar to the one previously mentioned, except for the fact that it returns a dictionary with the alphabet on the outer disc being the keys and the letters on the inner disc are its values (compare with Figure 13). Moreover, the map contains both lower- and upper-case characters.

Time to code a character.

function code(c::Char, encryptionMap::Dict{Char, Char})::Char
    return get(encryptionMap, c, c)
end

To that end we used the built in get function that looks for a character (c, get’s second argument) in encryptionMap, if the search failed it returns the character as a default value (c, get’s third argument).

Finally, let’s code the message.

function code(msg::Str, rotBy::Int)::Str
    encryptionMap::Dict{Char, Char} = getEncryptionMap(rotBy)
    coderFn(c::Char)::Char = code(c, encryptionMap)
    return map(coderFn, msg)
end

code (generic function with 2 methods)

Notice, that we defined two different versions (aka methods) of code function. Julia will choose the right one during the invocation based on the type of the arguments.

Time for a test.

codeMsg(codedTxt, -13) == code(codedTxt, -13)

true

Works the same, still in the above case codeMsg(codedTxt, -13) takes tens of milliseconds to execute, whereas code(codedTxt, -13) only hundreds of microseconds (on my laptop). The human may not tell the difference, but we obtained some 50x speedup thanks to the faster lookups in dictionaries (sometimes called hash maps in other programming languages) and the fact that we do not generate our discs anew for every letter we code.