23.2 Solution

OK, so the technique relies on applying different Caesar cipher to every letter of the plain text. The shift used by the Caesar cipher is established by using the provided passphrase. Therefore, we can safely reuse some of the code from our previous solution (see Section 22.2).

function getAlphabets(rotBy::Int, upper::Bool)::Tuple{Str, Str}
    alphabet::Str = upper ? join('A':'Z') : join('a':'z')
    rot::Int = abs(rotBy) % length(alphabet)
    rotAlphabet::Str = alphabet[(rot+1):end] * alphabet[1:rot]
    return rotBy < 0 ? (rotAlphabet, alphabet) : (alphabet, rotAlphabet)
end

function codeChar(c::Char, rotBy::Int)::Char
    outerDisc::Str, innerDisc::Str = getAlphabets(rotBy, isuppercase(c))
    ind::Union{Int, Nothing} = findfirst(c, outerDisc)
    return isnothing(ind) ? c : innerDisc[ind]
end

Time to create a function that will (de)code the whole message.

function isAsciiLetter(c::Char)::Bool
    return isascii(c) && isletter(c)
end

function codeMsg(msg::Str, passphrase::Str, decode::Bool=false)::Str
    pass::Str = filter(isAsciiLetter, lowercase(passphrase))
    pwr::Int = ceil(length(msg) / length(pass))
    pass = pass ^ pwr
    shifts::Vec{Int} = [c - 'a' for c in pass]
    if decode
        shifts .*= -1
    end
    result::Vec{Char} = Vec{Char}(undef, length(msg))
    shiftsInd::Int = 1
    for (ind, char) in enumerate(msg)
        result[ind] = codeChar(char, shifts[shiftsInd])
        if isAsciiLetter(char)
            shiftsInd += 1
        end
    end
    return result |> join
end

We begin with come preparatory code. First, we lowercase the passphrase and retain only ‘a’:‘z’ characters (isAsciiLetter). Next, we check how many times longer is the coded message (length(msg)) in comparison to the passphrase (length(pass)). The ceil function rounds the obtained float to the nearest whole number higher than or equal to it. Finally, we repeat pass the necessary number of times (^ pwr) to make sure it is at least as long as our msg. Next, we obtain the shifts by subtracting 'a' from every character (c) in the passphrase (pass). For decoding (if decode) purposes we change the signs in shifts to the opposite (.*= -1, where .* multiplies every shift by -1 and = re-assigns them to the shifts variable). We initialize an empty vector of chars of a given length (Vec{Char}(undef, length(msg))). Afterwards, we traverse (for) all characters (char) and their indices (ind) in msg. We code a char with the proper shift (shiftsInd). If the coded character was a letter (isAsciiLetter(char)) we update the shiftsInd (we use the next shift for coding of another letter). Finally, we concatenate the chars (result) into a string (join) that we return.

Time for our minimal test.

(
    codeMsg("attacking tonight", "oculorhinolaryngology"),
    codeMsg("Attacking tonight", "oculorhinolaryngology"),
    codeMsg("attacking Tonight", "oCulorhinolaryngoloGY")
)

("ovnlqbpvt hznzeuz", "Ovnlqbpvt hznzeuz", "ovnlqbpvt Hznzeuz")

Yep, we got the expected “ovnlqbpvt hznzeuz” (with casing consistent with the original message).

And now for the second part of this exercise. We will code genesis.txt with the passphrase “Julia rocks, believe in its magic.” and see if it changed the frequency distribution of the letters (no single, clearly dominant letter).

To this end we will mostly use the code from Section 21.2 so go there if you need detailed explanations.

First, lets read the text in and encode it.

# adjust the file path if necessary
# genesis.txt ~31 KiB
plainTxt = open("./code_snippets/vigenere/genesis.txt") do file
    read(file, Str)
end
passphrase = "Julia rocks, believe in its magic."
codedTxt = codeMsg(plainTxt, passphrase)

(
    first(plainTxt, 16),
    first(codedTxt, 16),
)

("In the beginning", "Rh epe ssisfomyo")

Now let’s use the functions to obtain the letter frequencies.

plainTxt = filter(isAsciiLetter, uppercase(plainTxt))
codedTxt = filter(isAsciiLetter, uppercase(codedTxt))

function getCounts(s::Str)::Dict{Char,Int}
    counts::Dict{Char, Int} = Dict()
    for char in s
        if haskey(counts, char)
            counts[char] = counts[char] + 1
        else
            counts[char] = 1
        end
    end
    return counts
end

function getFreqs(counts::Dict{Char, Int})::Dict{Char,Flt}
    total::Int = sum(values(counts))
    return Dict(k => v/total for (k, v) in counts)
end

function getFreqs(s::Str)::Dict{Char,Flt}
    return s |> getCounts |> getFreqs
end

And finally, cherry on the cake. Instead of just printing the percentages, we will draw the comparison of the letters distribution in both texts.

import CairoMakie as Cmk

function drawFreqComparison(txt1::Str, title1::Str,
                            txt2::Str, title2::Str)::Cmk.Figure
    letFreqs1::Dict{Char, Flt} = getFreqs(txt1)
    letFreqs2::Dict{Char, Flt} = getFreqs(txt2)
    alphabet::Str = join('A':'Z')
    revAlphabet::Str = alphabet[end:-1:1]
    len::Int = length(alphabet)
    freqs1::Vec{Flt} = [get(letFreqs1, c, 0) for c in alphabet]
    freqs2::Vec{Flt} = [get(letFreqs2, c, 0) for c in alphabet]
    fig::Cmk.Figure = Cmk.Figure(size=(600, 1200))
    ax1::Cmk.Axis = Cmk.Axis(fig[1, 1], title=title1,
                             xlabel="Frequency in text", ylabel="Letter",
                             yticks=(1:len, split(revAlphabet, "")),
                             ygridvisible=false)
    ax2::Cmk.Axis = Cmk.Axis(fig[2, 1], title=title2,
                             xlabel="Frequency in text", ylabel="Letter",
                             yticks=(1:len, split(revAlphabet, "")),
                             ygridvisible=false)
    Cmk.linkyaxes!(ax1, ax2)
    Cmk.linkxaxes!(ax1, ax2)
    Cmk.barplot!(ax1, len:-1:1, freqs1, color=:deepskyblue3, direction=:x)
    Cmk.barplot!(ax2, len:-1:1, freqs2, color=:deepskyblue3, direction=:x)
    return fig
end

drawFreqComparison(plainTxt, "genesis.txt in plain text",
                   codedTxt, "genesis.txt coded with a Vigenere cipher")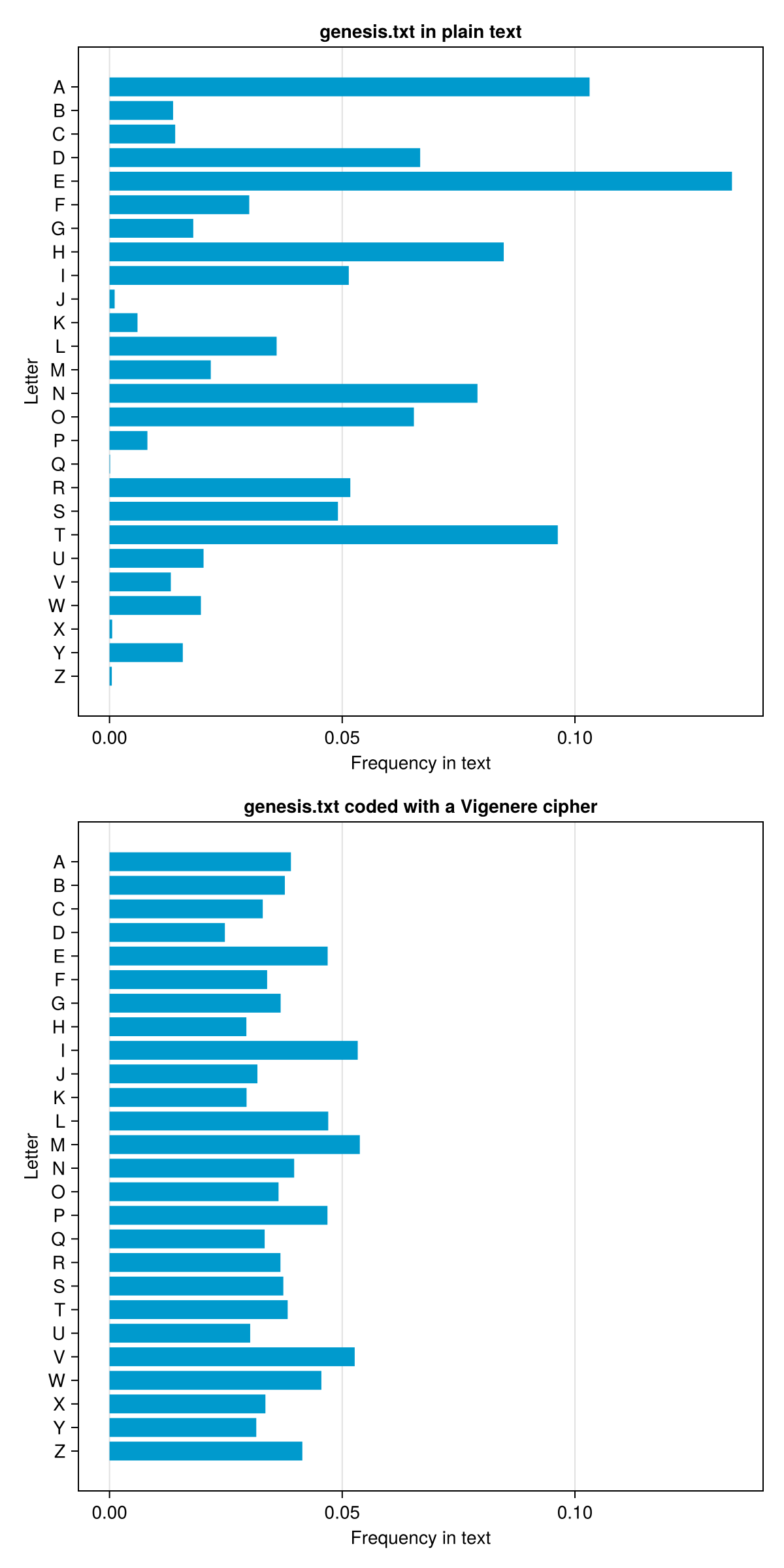

The letter distribution definetely got more uniform. This should make cracking the cipher more difficult, but still possible.

The performance of our codeMsg should be comparable to its counterpart in Section 22.2. If you expect to work on long text messages you may improve it, e.g. by generating encryptionMaps. It would be a Dict{Int, Dict{Char, Char}} where the key (Int) is a possible shift (0 to 25) and the value (Dict{Char, Char}) is an encryptionMap (like the one produced by getEncryptionMap in Section 22.2) for that shift. You could generate the encryptionMaps only once and use them inside codeMsg based on the shift from shifts::Vec{Int}. I’ll leave this as an extra exercise for you.