4.3 Probability - properties

One of the cool and practical stuff that I learned about probability is that it can be:

• added
• subtracted
• multiplied
• divided (not discussed in this section)

How about I illustrate that with a simple example.

From biology classes I remember that the genetic material (DNA) of a cell is in its nucleus. It is organized in a set of chromosomes. Chromosomes come in pairs (twin or homologous chromosomes, we get one from each of our parents). Each chromosome contains genes (like beads on a thread). Since we got a pair of chromosomes, then each chromosome from a pair contains a copy of the same gene(s). The copies are exactly the same or are different versions of a gene (we call them alleles). In order to create gametes (like the egg cell and sperm cells) the parents’ cells undergo division (meiosis). During this process a cell splits in two and each of the child cells gets one chromosome from the pair.

For instance chromosome 9 contains the genes that determine our ABO blood group system. A meiosis process for a person with blood group AB would look something like this (for simplicity I drew only twin chromosomes 9 and only genes for ABO blood group system).

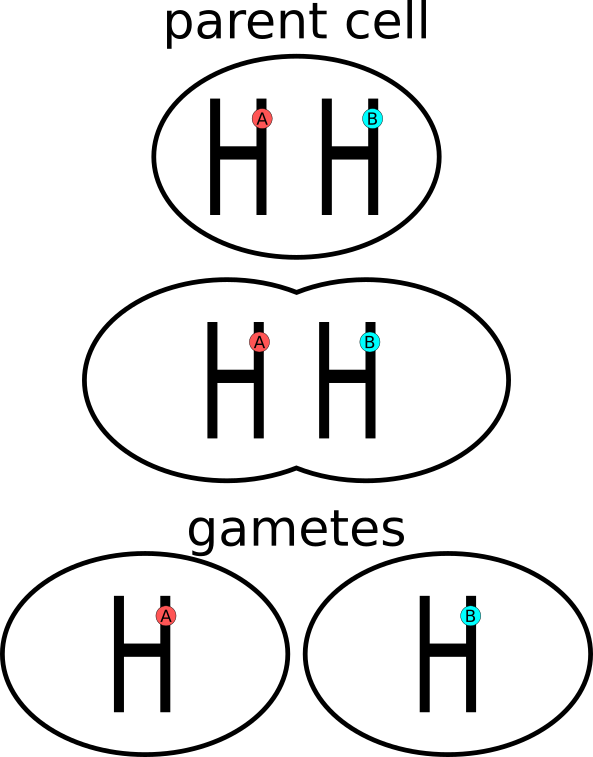
OK, let’s see how the mathematical properties of probability named at the beginning of this sub-chapter apply here.

But first, a warm-up (or a reminder if you will). In the previous part (see Section 4.2) we said that probability may be seen as a percentage, decimal or fraction. I think that the last one will be particularly useful to broaden our understanding of the concept. To determine probability of an event in the numerator (top) we insert the number of times that a particular event may happen, in the denominator (bottom) we place the number of all possible events, like so:

\(\frac{num\ times\ this\ event\ may\ happen}{num\ times\ any\ event\ may\ happen}\)

Let’s test this in practice with a few short Q&As (there may be some repetitions, but they are on purpose).


Q1. In the case illustrated in Figure 1 what is the probability of getting a gamete with allele C [for short I’ll name it P(C)] from a person with blood group AB?

A1. Since we can only get allele A or B, but no C then \(P(C) = \frac{0}{2} = 0\) (it is an impossible event).


Q2. In the case illustrated in Figure 1 what is the probability of getting a gamete with allele A [for short I’ll name it P(A)] from a person with blood group AB?

A2. Since we can get only allele A or B then A is 1 of 2 possible events, so \(\frac{1}{2} = 0.5\).

It seems that to answer this question we just had to divide the counts of the events satisfying our requirements by the counts of all events.

Note: This is exactly the same probability (since it relies on the same reasoning) as for getting a gamete with allele B (1 of 2 or \(\frac{1}{2} = 0.5\))

Q3. In the case illustrated in Figure 1, what is the probability of getting a gamete with allele A or B [for short I’ll name it P(A or B)] from a person with blood group AB?

A3. Since we can only get allele A or B then A or B are 2 events (1 event when A happens + 1 event when B happens) of 2 possible events, so

\(P(A\ or\ B) = \frac{1+1}{2} = \frac{2}{2} = 1\).

It seems that to answer this question we just had to add the counts of the both events.

Let’s look at it from a slightly different perspective.

Do you remember that in A2 we stated that the probability of getting gamete A is \(\frac{1}{2}\) and the probability of getting gamete B is \(\frac{1}{2}\)? And do you remember that in primary school we learned that fractions can be added one to another? Let’s see will that do us any good here.

\(P(A\ or\ B) = P(A) + P(B) = \frac{1}{2} + \frac{1}{2} = \frac{2}{2} = 1\)

Interesting, the answer (and calculations) are (virtually) the same despite a slightly different reasoning. So it seems that in this case the probabilities can be added.


Q4. In the case illustrated in Figure 1, what is the probability of getting a gamete with allele B (for short I’ll name it P(B)) from a person with blood group AB?

A4. I know, we already answered it in A2. But let’s do something wild and use a slightly different reasoning.

Getting gamete A or B are two incidents of two possible events (2 of 2). If we subtract event A (that we are not interested in) from both the events we get:

\(P(B) = \frac{2-1}{2} = \frac{1}{2}\)

It seems that to answer this question we just had to subtract the count of the events we are not interested in from the counts of the both events.

Let’s see if this works with fractions (aka probabilities).

\(P(B) = P(A\ or\ B) - P(A) = \frac{2}{2} - \frac{1}{2} = \frac{1}{2}\)

Yep, a success indeed.


Q5. Look at Figure 2.

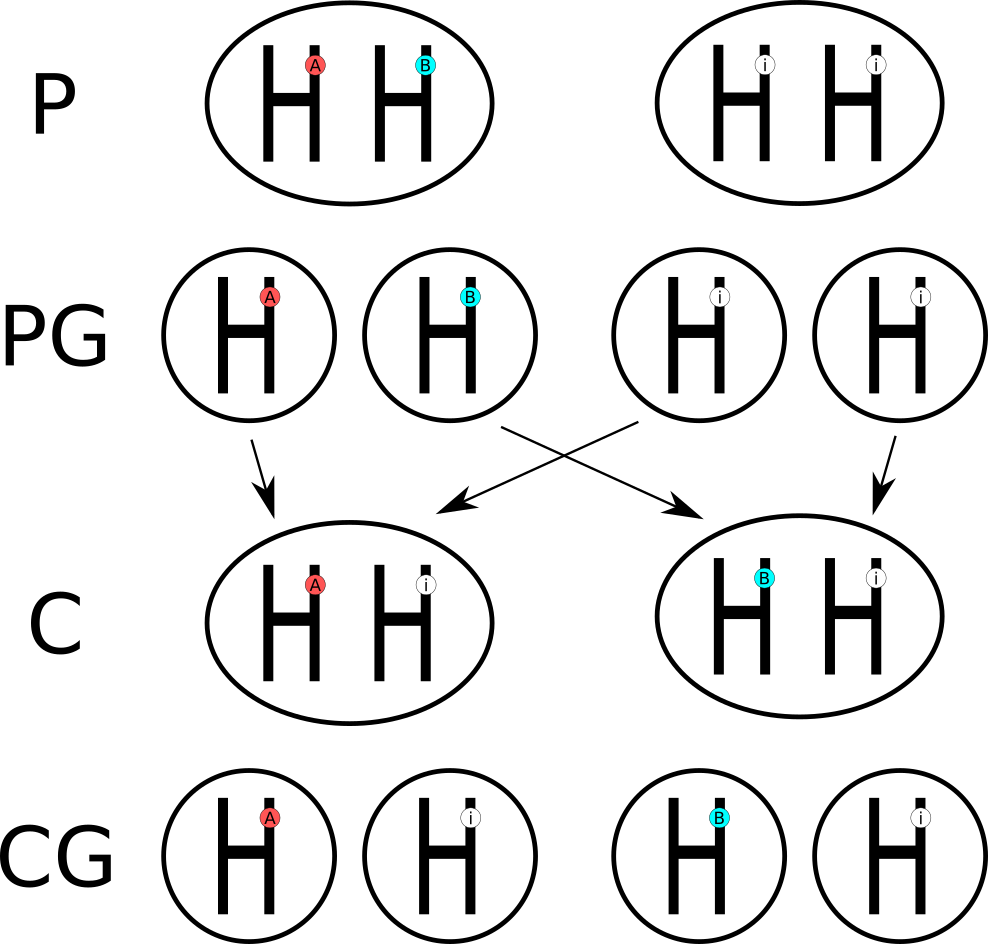
Here we see that a person with blood group AB got children with a person with blood group O (ii - recessive homo-zygote). The two possible blood groups in children are A (Ai - hetero-zygote) and B (Bi - hetero-zygote).

And now, the question. In the case illustrated in Figure 2, what is the probability that a child (row C) of those parents (row P) will produce a gamete with allele A (row CG)?

A5. One way to answer this question would be to calculate the gametes in the last row (CG). We got 4 gametes in total (A, i, B, i) only one of which fulfills the criteria (gamete with allele A). Therefore, the probability is

\(P(A\ in\ CG) = \frac{1}{4} = 0.25\) and that’s it.

Another way to think about this problem is the following. In order for a child to produce a gamete with allele A it had to get it first from the parent. So what we are looking for is:

1. what proportion of children got allele A from their parents (here, half of them)
2. in the children with allele A in their genotype, what proportion of gametes contains allele A (here, half of the gametes)

So, in order to get the half of the half we have to multiply two proportions (aka fractions):

\(P(A\ in\ CG) = P(A\ in\ C) * P(A\ in\ gametes\ of\ C\ with\ A)\)

\(P(A\ in\ CG) = \frac{1}{2} * \frac{1}{2} = \frac{1}{4} = 0.25\)

So it turns out that probabilities can be multiplied (at least sometimes).

4.3.1 Probability properties - summary

The above was my interpretation of the probability properties explained with biological examples instead of the standard fair coins tosses (not the perfect analogy though, since the events are not quite independent). Let’s sum up of what we learned. I’ll do this on a coin toss examples (outcome: heads or tails), you compare it with the examples from Q&As above.

1. Probability of an event is a proportion (or fraction) of times this event happens to the total amount of possible distinctive events. Example: \(P(heads) = \frac{heads}{heads + tails} = \frac{1}{2} = 0.5\)

2. Probability of an impossible event is equal to 0. Probability of a certain event is equal to 1. So, the probability takes values between 0 (inclusive) and 1 (inclusive).

3. Probabilities of the mutually exclusive complementary events add up to 1. Example: \(P(heads\ or\ tails) = P(heads) + P(tails) = \frac{1}{2} + \frac{1}{2} = 1\)

4. Probability of two mutually exclusive complementary events occurring at the same time is 0 (cannot get both heads and tails in a single coin toss).

5. Probability of two mutually exclusive complementary events occurring one after another is a product of two probabilities.

   Example: probability of getting two tails in two consecutive coin tosses \(P(tails\ and\ tails) = P(tails\ in\ 1st\ toss) * P(tails\ in\ 2nd\ toss)\)

   \(P(tails\ and\ tails) = \frac{1}{2} * \frac{1}{2} = \frac{1}{4} = 0.25\)

   Actually, the last is also true for two simultaneous coin tosses (imagine that one coin lands on a floor a few milliseconds before the other). Moreover, notice that here, the result of the first coin toss does not influence the result of the second coin toss (they are independent).

Anyway, the chances are that whenever you say P(this) AND P(that) you should use multiplication. Whereas whenever you say P(this) OR P(that) you ought to use addition. Of course you should always think does it make sense before you do it (if the events are not mutually exclusive and independent then it may not). To check your reasoning it may be easier to think about counts and their proportions. The latter can be translated to probabilities.